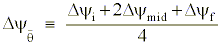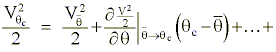Appendix C

The energy balance equation inclusive of the heat (q) added or subtracted during condensation or evaporation is given by (Reiter, 1972):

where y defines the Montgomery stream function (C_pT + gz) analyzed upon the initial (reference level) potential temperature surface (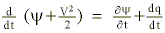). The entropy change during the diabatic process is

where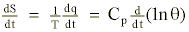

expresses the first law of thermodynamics in an isentropic coordinate system. To illustrate the positive diabatic trajectory solution, we integrate the energy balance expression during the time history of the air parcel as it condenses 100% of its water vapor: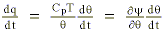

We once again use a Taylor expansion as in Appendix A to approximate to change of static and kinetic energies resulting during the diabatic process: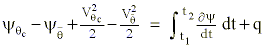

or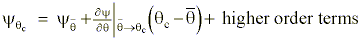

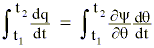
The offsetting effect of changes in the static energy field resulting from the total time differentials of y and q leave us with:

which states that a realization of the positive and negative diabatic potential results in important changes in the kinetic energy which must be evaluated along the quasi-Lagrangian path of the parcel as it goes from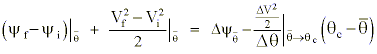 to q_c. In contrast, static energy changes need only be evaluated upon the original constant entropy surface () where the initial adiabatic trajectory is calculated. Local changes of y have been found to vary little with q, and may therefore be approximated by

where the subscripts refer to the parcel's initial, mid-, and final points along the trajectory.